HomeTurtlegraficsGPanelRobotics WebTigerPython
 Python - Online
sound
Deutsch   English   

16. SOUND

 

 

YOU LEARN HERE...

 

how the Turtle can play different sounds and melodies and even draw figures.

 

 

TONE FREQEUENCIES
 

To play different tones, use the function
playTone(frequency, duration).
The first parameter determines the audio frequency in Hz (heart), the second parameter the playback duration in milliseconds.Here are some sound frequencies:

Tone Frequency Tone Frequency Tone Frequency
c 131 c' 262 c'' 524
d 147 d' 294 d'' 588
e 165 e' 330 e'' 650
f 175 f' 349 f'' 698
g 196 g' 392 g'' 784
a 220 a' 440 a'' 880
h 247 h' 494 h''' 988

In order to tune instruments, Tone a' with a frequency of 440 Hz was defined as the concert pitch.The other frequencies can be calculated. The frequencies in the table are rounded.

 

 

EXAMPLES

 

Example 1: Playing a short melody
 To play several tones in succession, you can summarise the corresponding frequencies in a list. Use a for loop to go through the list and play the tones witht playTone(frequency, duration).

Program: 

from gturtle import *
      
song = [262, 294, 330, 349, 392, 392, 392, 0, 440, 440, 440, 440, 392]

for f in song:
    playTone(f, 250)
► Copy to clipboard

 

Example 2: Set tones with tone names
Instead of the frequencies, you can also specify the tones with letters: c‘, d’, e‘.... or an octave higher c’‘, d’‘, e’' ...

Program: 

from gturtle import *
    
song = ["c'","d'","e'","f'","g'","g'","g'",0,"a'","a'","a'","a'","g'"]
song2 = ["c''","d''","e''","f''","g''","g''","g''",0,"a''","a''",
         "a''","a''","g''"]

for f in song:
    playTone(f, 250)
delay(1000)
for f in song2:
    playTone(f, 250)
► Copy to clipboard

 

Example 3: Playing tones and drawing at the same time

The Turtle draws a staircase and plays increasingly higher tones. The function playTone(f, 500) is blocking, the programme waits at each step 500 ms until the tone has finished playing and only then begins to draw the next step. If you want the tone to be played and drawn at the same time, you must use the non-blocking function
playTone(f, 500, block = False).

 

Program: 

from gturtle import *

def step():    
    forward(20) 
    right(90)
    forward(30) 
    left(90)   
      
song = [262, 294, 330, 349, 392, 440, 494, 524]
for f in song:
    playTone(f, 500, block = False)
    #playTone(f, 500)
    step()
► Copy to clipboard

 

Example 4: Play several tones simultaneously
You want to play three tones simultaneously (C dur accord). Here, too, you must use the non-blocking function playTone().

Program: 

from gturtle import *

playTone(262, 2000, block = False)
playTone(330, 2000, block = False)
playTone(392, 2000, block = False)
► Copy to clipboard

 

Example 5: Choose different musical instruments
Mit der Funktion playTone(frequency, duration, intrument) kannst du zum Abspielen verschiedene Intrumente wählen: Klavier, Gitarre, Trompete, Geige, Orgeln, Harfe (harp), Xylofon (xylophone).

Program: 

from gturtle import *

song = ["c'", "e'", "g'", "c''"]

for f in song:
    playTone(f, 600, instrument="piano")
for f in song:
    playTone(f, 600, instrument="guitar")
for f in song:
    playTone(f, 600, instrument="trumpet")
for f in song:
    playTone(f, 600, instrument="violin")
for f in song:
    playTone(f, 600, instrument="organ")
► Copy to clipboard

 

Example 6: Simple piano
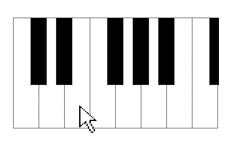
Using two for loops, you first draw the white and black keys of an octave. You can play a melody by clicking the mouse. Use the x-coordinate of the mouse click to calculate which key was clicked. For the black keys, you also use the getPixelColorStr() function, which returns the colour of the backgroud  

Program: 

from gturtle import *

def drawPiano():
    setPenColor("black")
    for x in range(-200, 160, 50):
        setPos(x, -100)
        for k in range(2):
            fd(216).rt(90).fd(50).rt(90)
    setPenWidth(32)
    for x in [-150, -100, 0, 50, 100, 200]:
        setPos(x, 0)
        fd(100)

def onMousePressed(x, y):
    if x > -200 and x < 215 and y > -100 and y < 100:
        i = int((x + 200)/50)
        setPos(x, y)
        if getPixelColorStr() == "black":
            k = int((x + 215) / 50)
            f = blacktones[k]
        else:
            f = whitetones[i]
        playTone(f, 400, block = False)

whitetones = [262, 294, 330, 349, 392, 440, 494, 524]
blacktones = [0, 277, 311, 0, 360, 415, 466, 0, 555]

makeTurtle(mousePressed = onMousePressed)
hideTurtle()
drawPiano()
addStatusBar(20)
setStatusText("Click a piano key to play!")
► Copy to clipboard

 

 

REMEMBER...
 

The Turtle can play tones using the function playTone(frequency, duration, instrument). If you want the Turtle to draw at the same time, or if you want to play several tones (chords) at the same time, use the non-blocking function playTone(frequency, duration, block = False).

 

 

TO SOLVE BY YOURSELF

 
1.

Add more notes to example 1 so that the song is played in its entirety.
2. Play the C dur scale (c, d, e, f, g, a, h, c) with different instruments.

3. With for f in reversed(song): you can play the notes in reverse order. Play the scale from exercise 2 first upwards and then back in reverse order. Try it with other melodies too.
4.

a) Play the 8 notes of the C major scale and draw larger and larger squares.

b) Play the 8 notes in reverse order and also draw the squares in reverse order (largest square first).

  
5. Add a second octave to the piano in example 5. Choose the tone names c, d, e, ..., c‘, d’, e‘, f’, ... c‘’ for the white keys and c#, d#, f#, g#, a#,c#‘, d#’, f#‘, g#’, a#' for the black keys.

   
16-1

Technical information:

These frequencies can be calculated. If you start from a fundamental tone (a‘ with f = 440 Hz), you obtain the frequency of the following semitone with the factor 1.05946 and the next whole tone with the factor 1.05946 * 1.05946 ≈ 1.122. (e.g. h’ = 440 * 1.122 = 494). The frequencies in the table are rounded.

Why these factors? An octave (frequency ratio c‘’ : c' = 2 : 1) is divided into twelve semitone steps.
One semitone = 1/12 octave. This corresponds to the frequency ratio = twelfth root of 2 = 1.05946.

 
16-2
Informations:

In English notation, notes are indicated with capital letters.

c, d, e, f ... corresponds to C3, D3, E3, F3,...
c', d', e', f'... corresponds toC4, D4, E4, F4, ...
c'', d'', e'', f'', corresponds toC5, D6, E5, F5, ...